3.4. Shor’s algorithm#
3.4.1. Background#
The goal of Shor’s algorithm is to factorize an integer \(N\) into the product of two smaller integers. Given an integer \(a\) coprime to \(N\), we want to find a power \(p\) such that \(a^p \mod N = 1\). The condition can be reformulated as \((a^{p/2}+1)(a^{p/2}-1) = mN\), where m is an integer. If either \((a^{p/2}+1)\) or \((a^{p/2}-1)\) shares a nontrivial factor with \(N\), then we successfully factorize \(N\). Otherwise, we choose another \(a\) and start over.
3.4.2. Implementation in geqo#
Shor’s algorithm is part of geqo’s algorithm library. The function can be imported from geqo.algorithms and it can be called with Shor(N, a) where \(N\) is the number to be factorized and a is the number for which the order \(p\) has to be found. The function generates a quantum circuit that corresponds to Shor’s algorithm with the chosen parameters.
3.4.3. Example for Shor’s algorithm#
In the following example, we factorize \(N= 15\) and we choose \(a =7\).
from geqo.algorithms import Shor, InverseQFT
from geqo.simulators import simulatorStatevectorNumpy, statevectorSimulatorCuPy
from geqo.visualization import plot_mpl
from geqo.utils import bin2num
First, we generate the quantum circuit and we show the corresponding circuit diagram.
shor = Shor(N=15, a=7)
plot_mpl(shor, style="jos")
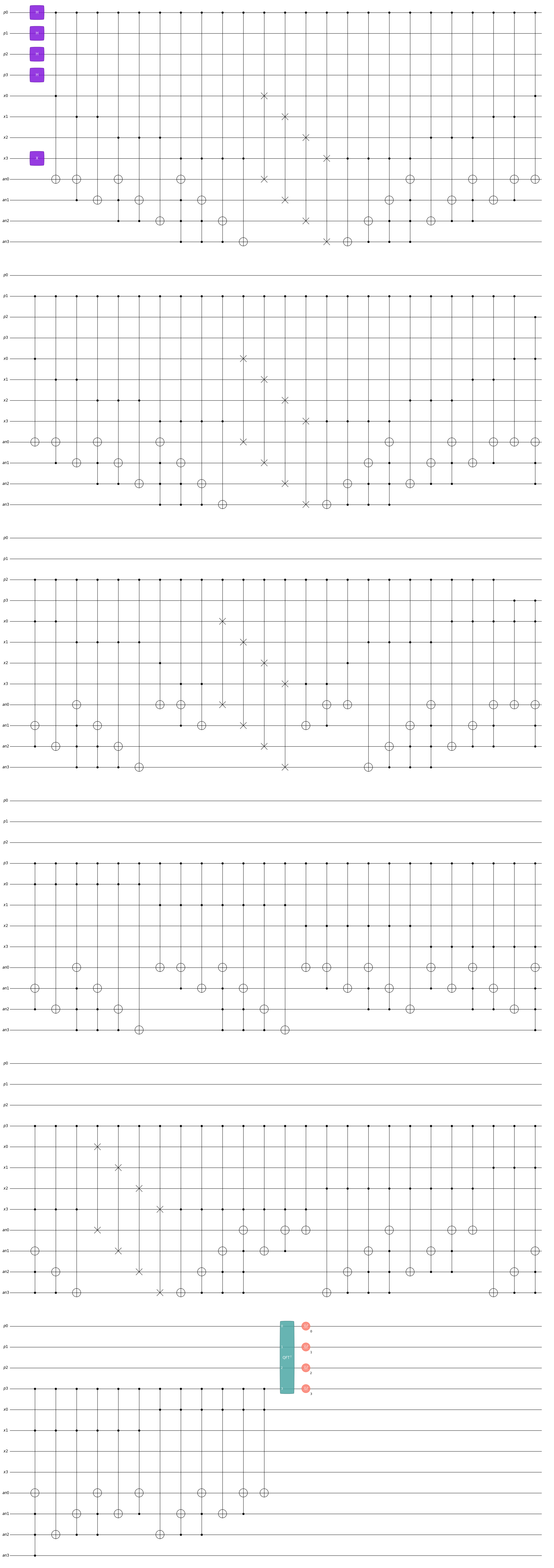
In the following, the circuit is simulated with simulatorStatevectorNumpy. As the constructed circuit uses a QFT, we have to call the prepareBackend function with the appropriate QFT.
sim = simulatorStatevectorNumpy(12, 4)
sim.prepareBackend([InverseQFT(4)])
sim.apply(shor, [*range(12)], [*range(4)])
sim.measurementResult
{(0, 0, 0, 0): np.float64(0.24999999999999967),
(0, 0, 0, 1): np.float64(0.0),
(0, 0, 1, 0): np.float64(0.0),
(0, 0, 1, 1): np.float64(0.0),
(0, 1, 0, 0): np.float64(0.24999999999999967),
(0, 1, 0, 1): np.float64(0.0),
(0, 1, 1, 0): np.float64(0.0),
(0, 1, 1, 1): np.float64(0.0),
(1, 0, 0, 0): np.float64(0.24999999999999967),
(1, 0, 0, 1): np.float64(0.0),
(1, 0, 1, 0): np.float64(0.0),
(1, 0, 1, 1): np.float64(0.0),
(1, 1, 0, 0): np.float64(0.24999999999999967),
(1, 1, 0, 1): np.float64(0.0),
(1, 1, 1, 0): np.float64(0.0),
(1, 1, 1, 1): np.float64(0.0)}
3.4.4. Classical post-processing#
The measurement results of the simulation can be used by the following post-processing procedure to derive the factors of \(N\).
from fractions import Fraction
from math import gcd
measured = []
for key, item in sim.measurementResult.items():
if item > 1e-5:
measured.append(bin2num(key) / 2**4)
print("[1/p, 2/p, ..., (p-1)/p] :", measured)
x = measured[1] - measured[0]
f = Fraction(x).limit_denominator()
p = f.denominator
print("hidden period p = ", p)
gcd1 = gcd(int(7 ** (p / 2) + 1), 15)
gcd2 = gcd(int(7 ** (p / 2) - 1), 15)
if gcd1 != 1:
factor1 = gcd1
factor2 = int(15 / gcd1)
else:
factor1 = gcd2
factor2 = int(15 / gcd2)
if (factor1, factor2) in [(1, 15), (15, 1)]:
print("Choose another 'a' and run the Shor's algorithm again.")
else:
print(f"15 can be factored into {factor1} * {factor2}")
[1/p, 2/p, ..., (p-1)/p] : [0.0, 0.25, 0.5, 0.75]
hidden period p = 4
15 can be factored into 5 * 3
3.4.5. Factorize greater numbers with CuPy#
In the following example, we factorize \(N = 51\) and \(N= 111\) with statevectorSimulatorCuPy. We choose \(a = 5\) and \(a =11\) respectively.
from fractions import Fraction
from math import gcd
shor51 = Shor(51, 5)
sim = statevectorSimulatorCuPy(18, 6)
sim.prepareBackend([InverseQFT(6)])
sim.apply(shor51, [*range(18)], [*range(6)])
measured = []
for key, item in sim.measurementResult.items():
if item > 1e-5:
measured.append(bin2num(key) / 2**6)
x = measured[1] - measured[0]
f = Fraction(x).limit_denominator()
p = f.denominator
print("hidden period p = ", p)
gcd1 = gcd(int(5 ** (p / 2) + 1), 51)
gcd2 = gcd(int(5 ** (p / 2) - 1), 51)
if gcd1 != 1:
factor1 = gcd1
factor2 = int(51 / gcd1)
else:
factor1 = gcd2
factor2 = int(51 / gcd2)
if (factor1, factor2) in [(1, 51), (51, 1)]:
print("Choose another 'a' and run the Shor's algorithm again.")
else:
print(f"51 can be factored into {factor1} * {factor2}")
hidden period p = 16
51 can be factored into 17 * 3
from fractions import Fraction
from math import gcd
shor111 = Shor(111, 11)
sim = statevectorSimulatorCuPy(21, 7)
sim.prepareBackend([InverseQFT(7)])
sim.apply(shor111, [*range(21)], [*range(7)])
measured = []
for key, item in sim.measurementResult.items():
if item > 1e-5:
measured.append(bin2num(key) / 2**7)
x = measured[1] - measured[0]
f = Fraction(x).limit_denominator()
p = f.denominator
print("hidden period p = ", p)
gcd1 = gcd(int(11 ** (p / 2) + 1), 111)
gcd2 = gcd(int(11 ** (p / 2) - 1), 111)
if gcd1 != 1:
factor1 = gcd1
factor2 = int(111 / gcd1)
else:
factor1 = gcd2
factor2 = int(111 / gcd2)
if (factor1, factor2) in [(1, 111), (111, 1)]:
print("Choose another 'a' and run the Shor's algorithm again.")
else:
print(f"111 can be factored into {factor1} * {factor2}")
hidden period p = 128
111 can be factored into 3 * 37
3.4.6. Conversion to OpenQASM3 code#
The quantum circuit for Shor’s algorithm can be converted to OpenQASM3 code.
dshor = Shor(N=15, a=7, decompose=True)
code = sim.sequence_to_qasm3(dshor)
print(code)
OPENQASM 3.0;
include 'stdgates.inc';
qubit[12] q;
bit[4] c;
x q[x3];
h q[p0];
h q[p1];
h q[p2];
h q[p3];
ccx q[p0], q[x0], q[an0];
ccx q[an1], q[p1], q[an0];
ccx q[p0], q[x1], q[p1];
ccx q[an1], q[p1], q[an0];
ccx q[p0], q[x1], q[p1];
ccx q[p0], q[x1], q[an1];
ccx q[an2], q[p2], q[an0];
ccx q[an1], q[p1], q[p2];
ccx q[p0], q[x2], q[p1];
ccx q[an1], q[p1], q[p2];
ccx q[an2], q[p2], q[an0];
ccx q[an1], q[p1], q[p2];
ccx q[p0], q[x2], q[p1];
ccx q[an1], q[p1], q[p2];
ccx q[an2], q[p1], q[an1];
ccx q[p0], q[x2], q[p1];
ccx q[an2], q[p1], q[an1];
ccx q[p0], q[x2], q[p1];
ccx q[p0], q[x2], q[an2];
ccx q[an3], q[p3], q[an0];
ccx q[an2], q[p2], q[p3];
ccx q[an1], q[p1], q[p2];
ccx q[p0], q[x3], q[p1];
ccx q[an1], q[p1], q[p2];
ccx q[an2], q[p2], q[p3];
ccx q[an3], q[p3], q[an0];
ccx q[an2], q[p2], q[p3];
ccx q[an1], q[p1], q[p2];
ccx q[p0], q[x3], q[p1];
ccx q[an1], q[p1], q[p2];
ccx q[an2], q[p2], q[p3];
ccx q[an3], q[p2], q[an1];
ccx q[an2], q[p1], q[p2];
ccx q[p0], q[x3], q[p1];
ccx q[an2], q[p1], q[p2];
ccx q[an3], q[p2], q[an1];
ccx q[an2], q[p1], q[p2];
ccx q[p0], q[x3], q[p1];
ccx q[an2], q[p1], q[p2];
ccx q[an3], q[p1], q[an2];
ccx q[p0], q[x3], q[p1];
ccx q[an3], q[p1], q[an2];
ccx q[p0], q[x3], q[p1];
ccx q[p0], q[x3], q[an3];
ccx q[p0], q[x0], q[an0];
ccx q[p0], q[an0], q[x0];
ccx q[p0], q[x0], q[an0];
ccx q[p0], q[x1], q[an1];
ccx q[p0], q[an1], q[x1];
ccx q[p0], q[x1], q[an1];
ccx q[p0], q[x2], q[an2];
ccx q[p0], q[an2], q[x2];
ccx q[p0], q[x2], q[an2];
ccx q[p0], q[x3], q[an3];
ccx q[p0], q[an3], q[x3];
ccx q[p0], q[x3], q[an3];
ccx q[p0], q[x3], q[an3];
ccx q[an3], q[p1], q[an2];
ccx q[p0], q[x3], q[p1];
ccx q[an3], q[p1], q[an2];
ccx q[p0], q[x3], q[p1];
ccx q[an3], q[p2], q[an1];
ccx q[an2], q[p1], q[p2];
ccx q[p0], q[x3], q[p1];
ccx q[an2], q[p1], q[p2];
ccx q[an3], q[p2], q[an1];
ccx q[an2], q[p1], q[p2];
ccx q[p0], q[x3], q[p1];
ccx q[an2], q[p1], q[p2];
ccx q[an3], q[p3], q[an0];
ccx q[an2], q[p2], q[p3];
ccx q[an1], q[p1], q[p2];
ccx q[p0], q[x3], q[p1];
ccx q[an1], q[p1], q[p2];
ccx q[an2], q[p2], q[p3];
ccx q[an3], q[p3], q[an0];
ccx q[an2], q[p2], q[p3];
ccx q[an1], q[p1], q[p2];
ccx q[p0], q[x3], q[p1];
ccx q[an1], q[p1], q[p2];
ccx q[an2], q[p2], q[p3];
ccx q[p0], q[x2], q[an2];
ccx q[an2], q[p1], q[an1];
ccx q[p0], q[x2], q[p1];
ccx q[an2], q[p1], q[an1];
ccx q[p0], q[x2], q[p1];
ccx q[an2], q[p2], q[an0];
ccx q[an1], q[p1], q[p2];
ccx q[p0], q[x2], q[p1];
ccx q[an1], q[p1], q[p2];
ccx q[an2], q[p2], q[an0];
ccx q[an1], q[p1], q[p2];
ccx q[p0], q[x2], q[p1];
ccx q[an1], q[p1], q[p2];
ccx q[p0], q[x1], q[an1];
ccx q[an1], q[p1], q[an0];
ccx q[p0], q[x1], q[p1];
ccx q[an1], q[p1], q[an0];
ccx q[p0], q[x1], q[p1];
ccx q[p0], q[x0], q[an0];
ccx q[p1], q[x0], q[an0];
ccx q[an1], q[p0], q[an0];
ccx q[p1], q[x1], q[p0];
ccx q[an1], q[p0], q[an0];
ccx q[p1], q[x1], q[p0];
ccx q[p1], q[x1], q[an1];
ccx q[an2], q[p2], q[an0];
ccx q[an1], q[p0], q[p2];
ccx q[p1], q[x2], q[p0];
ccx q[an1], q[p0], q[p2];
ccx q[an2], q[p2], q[an0];
ccx q[an1], q[p0], q[p2];
ccx q[p1], q[x2], q[p0];
ccx q[an1], q[p0], q[p2];
ccx q[an2], q[p0], q[an1];
ccx q[p1], q[x2], q[p0];
ccx q[an2], q[p0], q[an1];
ccx q[p1], q[x2], q[p0];
ccx q[p1], q[x2], q[an2];
ccx q[an3], q[p3], q[an0];
ccx q[an2], q[p2], q[p3];
ccx q[an1], q[p0], q[p2];
ccx q[p1], q[x3], q[p0];
ccx q[an1], q[p0], q[p2];
ccx q[an2], q[p2], q[p3];
ccx q[an3], q[p3], q[an0];
ccx q[an2], q[p2], q[p3];
ccx q[an1], q[p0], q[p2];
ccx q[p1], q[x3], q[p0];
ccx q[an1], q[p0], q[p2];
ccx q[an2], q[p2], q[p3];
ccx q[an3], q[p2], q[an1];
ccx q[an2], q[p0], q[p2];
ccx q[p1], q[x3], q[p0];
ccx q[an2], q[p0], q[p2];
ccx q[an3], q[p2], q[an1];
ccx q[an2], q[p0], q[p2];
ccx q[p1], q[x3], q[p0];
ccx q[an2], q[p0], q[p2];
ccx q[an3], q[p0], q[an2];
ccx q[p1], q[x3], q[p0];
ccx q[an3], q[p0], q[an2];
ccx q[p1], q[x3], q[p0];
ccx q[p1], q[x3], q[an3];
ccx q[p1], q[x0], q[an0];
ccx q[p1], q[an0], q[x0];
ccx q[p1], q[x0], q[an0];
ccx q[p1], q[x1], q[an1];
ccx q[p1], q[an1], q[x1];
ccx q[p1], q[x1], q[an1];
ccx q[p1], q[x2], q[an2];
ccx q[p1], q[an2], q[x2];
ccx q[p1], q[x2], q[an2];
ccx q[p1], q[x3], q[an3];
ccx q[p1], q[an3], q[x3];
ccx q[p1], q[x3], q[an3];
ccx q[p1], q[x3], q[an3];
ccx q[an3], q[p0], q[an2];
ccx q[p1], q[x3], q[p0];
ccx q[an3], q[p0], q[an2];
ccx q[p1], q[x3], q[p0];
ccx q[an3], q[p2], q[an1];
ccx q[an2], q[p0], q[p2];
ccx q[p1], q[x3], q[p0];
ccx q[an2], q[p0], q[p2];
ccx q[an3], q[p2], q[an1];
ccx q[an2], q[p0], q[p2];
ccx q[p1], q[x3], q[p0];
ccx q[an2], q[p0], q[p2];
ccx q[an3], q[p3], q[an0];
ccx q[an2], q[p2], q[p3];
ccx q[an1], q[p0], q[p2];
ccx q[p1], q[x3], q[p0];
ccx q[an1], q[p0], q[p2];
ccx q[an2], q[p2], q[p3];
ccx q[an3], q[p3], q[an0];
ccx q[an2], q[p2], q[p3];
ccx q[an1], q[p0], q[p2];
ccx q[p1], q[x3], q[p0];
ccx q[an1], q[p0], q[p2];
ccx q[an2], q[p2], q[p3];
ccx q[p1], q[x2], q[an2];
ccx q[an2], q[p0], q[an1];
ccx q[p1], q[x2], q[p0];
ccx q[an2], q[p0], q[an1];
ccx q[p1], q[x2], q[p0];
ccx q[an2], q[p2], q[an0];
ccx q[an1], q[p0], q[p2];
ccx q[p1], q[x2], q[p0];
ccx q[an1], q[p0], q[p2];
ccx q[an2], q[p2], q[an0];
ccx q[an1], q[p0], q[p2];
ccx q[p1], q[x2], q[p0];
ccx q[an1], q[p0], q[p2];
ccx q[p1], q[x1], q[an1];
ccx q[an1], q[p0], q[an0];
ccx q[p1], q[x1], q[p0];
ccx q[an1], q[p0], q[an0];
ccx q[p1], q[x1], q[p0];
ccx q[p1], q[x0], q[an0];
ccx q[an2], q[p1], q[an0];
ccx q[an1], q[p0], q[p1];
ccx q[p2], q[x0], q[p0];
ccx q[an1], q[p0], q[p1];
ccx q[an2], q[p1], q[an0];
ccx q[an1], q[p0], q[p1];
ccx q[p2], q[x0], q[p0];
ccx q[an1], q[p0], q[p1];
ccx q[an2], q[p0], q[an1];
ccx q[p2], q[x0], q[p0];
ccx q[an2], q[p0], q[an1];
ccx q[p2], q[x0], q[p0];
ccx q[p2], q[x0], q[an2];
ccx q[an3], q[p3], q[an0];
ccx q[an2], q[p1], q[p3];
ccx q[an1], q[p0], q[p1];
ccx q[p2], q[x1], q[p0];
ccx q[an1], q[p0], q[p1];
ccx q[an2], q[p1], q[p3];
ccx q[an3], q[p3], q[an0];
ccx q[an2], q[p1], q[p3];
ccx q[an1], q[p0], q[p1];
ccx q[p2], q[x1], q[p0];
ccx q[an1], q[p0], q[p1];
ccx q[an2], q[p1], q[p3];
ccx q[an3], q[p1], q[an1];
ccx q[an2], q[p0], q[p1];
ccx q[p2], q[x1], q[p0];
ccx q[an2], q[p0], q[p1];
ccx q[an3], q[p1], q[an1];
ccx q[an2], q[p0], q[p1];
ccx q[p2], q[x1], q[p0];
ccx q[an2], q[p0], q[p1];
ccx q[an3], q[p0], q[an2];
ccx q[p2], q[x1], q[p0];
ccx q[an3], q[p0], q[an2];
ccx q[p2], q[x1], q[p0];
ccx q[p2], q[x1], q[an3];
ccx q[p2], q[x2], q[an0];
ccx q[an1], q[p0], q[an0];
ccx q[p2], q[x3], q[p0];
ccx q[an1], q[p0], q[an0];
ccx q[p2], q[x3], q[p0];
ccx q[p2], q[x3], q[an1];
ccx q[p2], q[x0], q[an0];
ccx q[p2], q[an0], q[x0];
ccx q[p2], q[x0], q[an0];
ccx q[p2], q[x1], q[an1];
ccx q[p2], q[an1], q[x1];
ccx q[p2], q[x1], q[an1];
ccx q[p2], q[x2], q[an2];
ccx q[p2], q[an2], q[x2];
ccx q[p2], q[x2], q[an2];
ccx q[p2], q[x3], q[an3];
ccx q[p2], q[an3], q[x3];
ccx q[p2], q[x3], q[an3];
ccx q[p2], q[x3], q[an1];
ccx q[an1], q[p0], q[an0];
ccx q[p2], q[x3], q[p0];
ccx q[an1], q[p0], q[an0];
ccx q[p2], q[x3], q[p0];
ccx q[p2], q[x2], q[an0];
ccx q[p2], q[x1], q[an3];
ccx q[an3], q[p0], q[an2];
ccx q[p2], q[x1], q[p0];
ccx q[an3], q[p0], q[an2];
ccx q[p2], q[x1], q[p0];
ccx q[an3], q[p1], q[an1];
ccx q[an2], q[p0], q[p1];
ccx q[p2], q[x1], q[p0];
ccx q[an2], q[p0], q[p1];
ccx q[an3], q[p1], q[an1];
ccx q[an2], q[p0], q[p1];
ccx q[p2], q[x1], q[p0];
ccx q[an2], q[p0], q[p1];
ccx q[an3], q[p3], q[an0];
ccx q[an2], q[p1], q[p3];
ccx q[an1], q[p0], q[p1];
ccx q[p2], q[x1], q[p0];
ccx q[an1], q[p0], q[p1];
ccx q[an2], q[p1], q[p3];
ccx q[an3], q[p3], q[an0];
ccx q[an2], q[p1], q[p3];
ccx q[an1], q[p0], q[p1];
ccx q[p2], q[x1], q[p0];
ccx q[an1], q[p0], q[p1];
ccx q[an2], q[p1], q[p3];
ccx q[p2], q[x0], q[an2];
ccx q[an2], q[p0], q[an1];
ccx q[p2], q[x0], q[p0];
ccx q[an2], q[p0], q[an1];
ccx q[p2], q[x0], q[p0];
ccx q[an2], q[p1], q[an0];
ccx q[an1], q[p0], q[p1];
ccx q[p2], q[x0], q[p0];
ccx q[an1], q[p0], q[p1];
ccx q[an2], q[p1], q[an0];
ccx q[an1], q[p0], q[p1];
ccx q[p2], q[x0], q[p0];
ccx q[an1], q[p0], q[p1];
ccx q[p3], q[x0], q[an0];
ccx q[an2], q[p1], q[an0];
ccx q[an1], q[p0], q[p1];
ccx q[p3], q[x0], q[p0];
ccx q[an1], q[p0], q[p1];
ccx q[an2], q[p1], q[an0];
ccx q[an1], q[p0], q[p1];
ccx q[p3], q[x0], q[p0];
ccx q[an1], q[p0], q[p1];
ccx q[an2], q[p0], q[an1];
ccx q[p3], q[x0], q[p0];
ccx q[an2], q[p0], q[an1];
ccx q[p3], q[x0], q[p0];
ccx q[p3], q[x0], q[an2];
ccx q[an3], q[p2], q[an0];
ccx q[an2], q[p1], q[p2];
ccx q[an1], q[p0], q[p1];
ccx q[p3], q[x0], q[p0];
ccx q[an1], q[p0], q[p1];
ccx q[an2], q[p1], q[p2];
ccx q[an3], q[p2], q[an0];
ccx q[an2], q[p1], q[p2];
ccx q[an1], q[p0], q[p1];
ccx q[p3], q[x0], q[p0];
ccx q[an1], q[p0], q[p1];
ccx q[an2], q[p1], q[p2];
ccx q[an3], q[p1], q[an1];
ccx q[an2], q[p0], q[p1];
ccx q[p3], q[x0], q[p0];
ccx q[an2], q[p0], q[p1];
ccx q[an3], q[p1], q[an1];
ccx q[an2], q[p0], q[p1];
ccx q[p3], q[x0], q[p0];
ccx q[an2], q[p0], q[p1];
ccx q[an3], q[p0], q[an2];
ccx q[p3], q[x0], q[p0];
ccx q[an3], q[p0], q[an2];
ccx q[p3], q[x0], q[p0];
ccx q[p3], q[x0], q[an3];
ccx q[p3], q[x1], q[an0];
ccx q[an1], q[p0], q[an0];
ccx q[p3], q[x1], q[p0];
ccx q[an1], q[p0], q[an0];
ccx q[p3], q[x1], q[p0];
ccx q[p3], q[x1], q[an1];
ccx q[an3], q[p2], q[an0];
ccx q[an2], q[p1], q[p2];
ccx q[an1], q[p0], q[p1];
ccx q[p3], q[x1], q[p0];
ccx q[an1], q[p0], q[p1];
ccx q[an2], q[p1], q[p2];
ccx q[an3], q[p2], q[an0];
ccx q[an2], q[p1], q[p2];
ccx q[an1], q[p0], q[p1];
ccx q[p3], q[x1], q[p0];
ccx q[an1], q[p0], q[p1];
ccx q[an2], q[p1], q[p2];
ccx q[an3], q[p1], q[an1];
ccx q[an2], q[p0], q[p1];
ccx q[p3], q[x1], q[p0];
ccx q[an2], q[p0], q[p1];
ccx q[an3], q[p1], q[an1];
ccx q[an2], q[p0], q[p1];
ccx q[p3], q[x1], q[p0];
ccx q[an2], q[p0], q[p1];
ccx q[an3], q[p0], q[an2];
ccx q[p3], q[x1], q[p0];
ccx q[an3], q[p0], q[an2];
ccx q[p3], q[x1], q[p0];
ccx q[p3], q[x1], q[an3];
ccx q[p3], q[x2], q[an0];
ccx q[an1], q[p0], q[an0];
ccx q[p3], q[x2], q[p0];
ccx q[an1], q[p0], q[an0];
ccx q[p3], q[x2], q[p0];
ccx q[p3], q[x2], q[an1];
ccx q[an2], q[p1], q[an0];
ccx q[an1], q[p0], q[p1];
ccx q[p3], q[x2], q[p0];
ccx q[an1], q[p0], q[p1];
ccx q[an2], q[p1], q[an0];
ccx q[an1], q[p0], q[p1];
ccx q[p3], q[x2], q[p0];
ccx q[an1], q[p0], q[p1];
ccx q[an2], q[p0], q[an1];
ccx q[p3], q[x2], q[p0];
ccx q[an2], q[p0], q[an1];
ccx q[p3], q[x2], q[p0];
ccx q[p3], q[x2], q[an2];
ccx q[an1], q[p0], q[an0];
ccx q[p3], q[x3], q[p0];
ccx q[an1], q[p0], q[an0];
ccx q[p3], q[x3], q[p0];
ccx q[p3], q[x3], q[an1];
ccx q[an2], q[p1], q[an0];
ccx q[an1], q[p0], q[p1];
ccx q[p3], q[x3], q[p0];
ccx q[an1], q[p0], q[p1];
ccx q[an2], q[p1], q[an0];
ccx q[an1], q[p0], q[p1];
ccx q[p3], q[x3], q[p0];
ccx q[an1], q[p0], q[p1];
ccx q[an2], q[p0], q[an1];
ccx q[p3], q[x3], q[p0];
ccx q[an2], q[p0], q[an1];
ccx q[p3], q[x3], q[p0];
ccx q[p3], q[x3], q[an2];
ccx q[an3], q[p2], q[an0];
ccx q[an2], q[p1], q[p2];
ccx q[an1], q[p0], q[p1];
ccx q[p3], q[x3], q[p0];
ccx q[an1], q[p0], q[p1];
ccx q[an2], q[p1], q[p2];
ccx q[an3], q[p2], q[an0];
ccx q[an2], q[p1], q[p2];
ccx q[an1], q[p0], q[p1];
ccx q[p3], q[x3], q[p0];
ccx q[an1], q[p0], q[p1];
ccx q[an2], q[p1], q[p2];
ccx q[an3], q[p1], q[an1];
ccx q[an2], q[p0], q[p1];
ccx q[p3], q[x3], q[p0];
ccx q[an2], q[p0], q[p1];
ccx q[an3], q[p1], q[an1];
ccx q[an2], q[p0], q[p1];
ccx q[p3], q[x3], q[p0];
ccx q[an2], q[p0], q[p1];
ccx q[an3], q[p0], q[an2];
ccx q[p3], q[x3], q[p0];
ccx q[an3], q[p0], q[an2];
ccx q[p3], q[x3], q[p0];
ccx q[p3], q[x3], q[an3];
ccx q[p3], q[x0], q[an0];
ccx q[p3], q[an0], q[x0];
ccx q[p3], q[x0], q[an0];
ccx q[p3], q[x1], q[an1];
ccx q[p3], q[an1], q[x1];
ccx q[p3], q[x1], q[an1];
ccx q[p3], q[x2], q[an2];
ccx q[p3], q[an2], q[x2];
ccx q[p3], q[x2], q[an2];
ccx q[p3], q[x3], q[an3];
ccx q[p3], q[an3], q[x3];
ccx q[p3], q[x3], q[an3];
ccx q[p3], q[x3], q[an3];
ccx q[an3], q[p0], q[an2];
ccx q[p3], q[x3], q[p0];
ccx q[an3], q[p0], q[an2];
ccx q[p3], q[x3], q[p0];
ccx q[an3], q[p1], q[an1];
ccx q[an2], q[p0], q[p1];
ccx q[p3], q[x3], q[p0];
ccx q[an2], q[p0], q[p1];
ccx q[an3], q[p1], q[an1];
ccx q[an2], q[p0], q[p1];
ccx q[p3], q[x3], q[p0];
ccx q[an2], q[p0], q[p1];
ccx q[an3], q[p2], q[an0];
ccx q[an2], q[p1], q[p2];
ccx q[an1], q[p0], q[p1];
ccx q[p3], q[x3], q[p0];
ccx q[an1], q[p0], q[p1];
ccx q[an2], q[p1], q[p2];
ccx q[an3], q[p2], q[an0];
ccx q[an2], q[p1], q[p2];
ccx q[an1], q[p0], q[p1];
ccx q[p3], q[x3], q[p0];
ccx q[an1], q[p0], q[p1];
ccx q[an2], q[p1], q[p2];
ccx q[p3], q[x3], q[an1];
ccx q[an1], q[p0], q[an0];
ccx q[p3], q[x3], q[p0];
ccx q[an1], q[p0], q[an0];
ccx q[p3], q[x3], q[p0];
ccx q[p3], q[x3], q[an0];
ccx q[p3], q[x2], q[an3];
ccx q[an3], q[p0], q[an2];
ccx q[p3], q[x2], q[p0];
ccx q[an3], q[p0], q[an2];
ccx q[p3], q[x2], q[p0];
ccx q[an3], q[p1], q[an1];
ccx q[an2], q[p0], q[p1];
ccx q[p3], q[x2], q[p0];
ccx q[an2], q[p0], q[p1];
ccx q[an3], q[p1], q[an1];
ccx q[an2], q[p0], q[p1];
ccx q[p3], q[x2], q[p0];
ccx q[an2], q[p0], q[p1];
ccx q[an3], q[p2], q[an0];
ccx q[an2], q[p1], q[p2];
ccx q[an1], q[p0], q[p1];
ccx q[p3], q[x2], q[p0];
ccx q[an1], q[p0], q[p1];
ccx q[an2], q[p1], q[p2];
ccx q[an3], q[p2], q[an0];
ccx q[an2], q[p1], q[p2];
ccx q[an1], q[p0], q[p1];
ccx q[p3], q[x2], q[p0];
ccx q[an1], q[p0], q[p1];
ccx q[an2], q[p1], q[p2];
ccx q[p3], q[x2], q[an2];
ccx q[an2], q[p0], q[an1];
ccx q[p3], q[x2], q[p0];
ccx q[an2], q[p0], q[an1];
ccx q[p3], q[x2], q[p0];
ccx q[an2], q[p1], q[an0];
ccx q[an1], q[p0], q[p1];
ccx q[p3], q[x2], q[p0];
ccx q[an1], q[p0], q[p1];
ccx q[an2], q[p1], q[an0];
ccx q[an1], q[p0], q[p1];
ccx q[p3], q[x2], q[p0];
ccx q[an1], q[p0], q[p1];
ccx q[p3], q[x2], q[an0];
ccx q[p3], q[x1], q[an3];
ccx q[an3], q[p0], q[an2];
ccx q[p3], q[x1], q[p0];
ccx q[an3], q[p0], q[an2];
ccx q[p3], q[x1], q[p0];
ccx q[an3], q[p1], q[an1];
ccx q[an2], q[p0], q[p1];
ccx q[p3], q[x1], q[p0];
ccx q[an2], q[p0], q[p1];
ccx q[an3], q[p1], q[an1];
ccx q[an2], q[p0], q[p1];
ccx q[p3], q[x1], q[p0];
ccx q[an2], q[p0], q[p1];
ccx q[an3], q[p2], q[an0];
ccx q[an2], q[p1], q[p2];
ccx q[an1], q[p0], q[p1];
ccx q[p3], q[x1], q[p0];
ccx q[an1], q[p0], q[p1];
ccx q[an2], q[p1], q[p2];
ccx q[an3], q[p2], q[an0];
ccx q[an2], q[p1], q[p2];
ccx q[an1], q[p0], q[p1];
ccx q[p3], q[x1], q[p0];
ccx q[an1], q[p0], q[p1];
ccx q[an2], q[p1], q[p2];
ccx q[p3], q[x1], q[an2];
ccx q[an2], q[p0], q[an1];
ccx q[p3], q[x1], q[p0];
ccx q[an2], q[p0], q[an1];
ccx q[p3], q[x1], q[p0];
ccx q[an2], q[p1], q[an0];
ccx q[an1], q[p0], q[p1];
ccx q[p3], q[x1], q[p0];
ccx q[an1], q[p0], q[p1];
ccx q[an2], q[p1], q[an0];
ccx q[an1], q[p0], q[p1];
ccx q[p3], q[x1], q[p0];
ccx q[an1], q[p0], q[p1];
ccx q[p3], q[x1], q[an1];
ccx q[an1], q[p0], q[an0];
ccx q[p3], q[x1], q[p0];
ccx q[an1], q[p0], q[an0];
ccx q[p3], q[x1], q[p0];
ccx q[p3], q[x0], q[an2];
ccx q[an2], q[p0], q[an1];
ccx q[p3], q[x0], q[p0];
ccx q[an2], q[p0], q[an1];
ccx q[p3], q[x0], q[p0];
ccx q[an2], q[p1], q[an0];
ccx q[an1], q[p0], q[p1];
ccx q[p3], q[x0], q[p0];
ccx q[an1], q[p0], q[p1];
ccx q[an2], q[p1], q[an0];
ccx q[an1], q[p0], q[p1];
ccx q[p3], q[x0], q[p0];
ccx q[an1], q[p0], q[p1];
ccx q[p3], q[x0], q[an1];
ccx q[an1], q[p0], q[an0];
ccx q[p3], q[x0], q[p0];
ccx q[an1], q[p0], q[an0];
ccx q[p3], q[x0], q[p0];
ccx q[p3], q[x0], q[an0];
swap q[0], q[3];
swap q[1], q[2];
h q[p3];
cp(-1.5707963267948966) q[p3], q[p2];
h q[p2];
cp(-0.7853981633974483) q[p3], q[p1];
cp(-1.5707963267948966) q[p2], q[p1];
h q[p1];
cp(-0.39269908169872414) q[p3], q[p0];
cp(-0.7853981633974483) q[p2], q[p0];
cp(-1.5707963267948966) q[p1], q[p0];
h q[p0];
measure q[p0] -> c[c0];
measure q[p1] -> c[c1];
measure q[p2] -> c[c2];
measure q[p3] -> c[c3];
print(
"number of basic gates (PauliX, Hadamard, Toffoli, Swap, controlled-Phase):",
len(dshor.gatesAndTargets),
)
number of basic gates (PauliX, Hadamard, Toffoli, Swap, controlled-Phase): 593
