4.4. Pattern replacer for geqo

4.4.1. Background

The pattern replacer is a tool that allows to automatically replace gates of a quantum circuit with other gates as specified by user-defined replacement rules, which we call pattern in the following.

For instance, two consecutive Pauli gates PauliX() on one qubit can be replaced by the idenitity. This means that Sequence([], [0], [(PauliX(), [0]), (PauliX(), [0])]) can be replaced by Sequence([], [0], []). These two sequences can be used to define a pattern.

The pattern replacer comes along with tools to identify parts of circuits, that are suitable for a replacement. For instance, if there is another gate between the two PauliX gates, but operates on another qubit, then this gate can be filtered out. Furthermore, the tool contains a unification algorithm to match the names of bits, qubits and parameters of gates, which allows patterns to be applied to quantum circuits that use different names for these items.

from geqo.core import Sequence
from geqo.core import BasicGate, InverseBasicGate
from geqo.gates import PauliX, CNOT, Hadamard
from geqo.visualization import plot_latex
from geqo.simulators import ensembleSimulatorSymPy
from geqo.algorithms import (
    Pattern,
    findLongestRunSequence,
    getAllLongestRuns,
    getAllRuns,
)

4.4.2. Example: Eliminate double PauliX

• a sequence of two PauliX gates can be reduced to no gates at all

• the pattern is defined with the input and the output sequence

inputSequence = Sequence([], [0], [(PauliX(), [0]), (PauliX(), [0])])
outputSequence = Sequence([], [0], [])
lambdas = []

pat = Pattern("test1", inputSequence, outputSequence, lambdas)
print(pat)

Pattern #bits/#quits=0/1 and #lamdbas=0

• the input pattern can be replaced with the output pattern with the function replacer

• the name of the qubit is automatically matched with the corresponding name in the pattern, which allows the pattern to be applied

seq = Sequence([], ["a"], [(PauliX(), ["a"]), (PauliX(), ["a"])])
newSeq, subst = pat.replacer(seq)
print("used subst=", subst)
print("newSeq=", newSeq)

check sequence
run ix= 0
set qubits 0 to value a
res1/res2= True {}
run ix= 1
res1/res2= True {}
res1/res2/resQ/resC= True {} {0: 'a'} {}
replace_recursion called for Sequence([], [0], [])
used subst= {}
newSeq= Sequence([], ['a'], [])

4.4.3. Example: Replace two BasicGates with another one

• two basic gates with the same number of qubits can be merged into a single basic gate

• the unitary operation corresponding to the new gate is the product of the two unitary operations of the two original gates

• the definition of the parameter of the new gate can be obtained with lambda functions

• the lambda functions can be used for the setValue function of simulators

inputSequence = Sequence(
    [], [0], [(BasicGate("x1", 1), [0]), (BasicGate("x2", 1), [0])]
)
outputSequence = Sequence([], [0], [(BasicGate("y1", 1), [0])])
lambdas = [("y1", lambda x1, x2: x2 * x1)]

pat = Pattern("test2", inputSequence, outputSequence, lambdas)
print(pat)

Pattern #bits/#quits=0/1 and #lamdbas=1

• the function replacer is used to apply the pattern

• the names x1 and x2 of the gates are automatically matched with the names a and b of the pattern

seq = Sequence([], [0], [(BasicGate("a", 1), [0]), (BasicGate("b", 1), [0])])
newSeq, subst = pat.replacer(seq)
print("used subst=", subst)
print("newSeq=", newSeq)

check sequence
run ix= 0
set qubits 0 to value 0
check basic gate
add pattern.name/target.name= x1 a
res1/res2= True {'x1': 'a'}
run ix= 1
check basic gate
add pattern.name/target.name= x2 b
res1/res2= True {'x1': 'a', 'x2': 'b'}
res1/res2/resQ/resC= True {'x1': 'a', 'x2': 'b'} {0: 0} {}
replace_recursion called for Sequence([], [0], [(BasicGate("y1", 1), [0])])
replace_recursion called for BasicGate("y1", 1)
replace basic gate
used subst= {'x1': 'a', 'x2': 'b'}
newSeq= Sequence([], [0], [(BasicGate("y1", 1), [0])])

4.4.4. Example: CNOT reversal with Hadamard gates

• a CNOT operation on qubits \(q_0\) and \(q_1\) can be turned into a CNOT on \(q_1\) and \(q_0\) by applying Hadamard gates before and after the gate

inputSequence = Sequence(
    [],
    [0, 1],
    [
        (Hadamard(), [0]),
        (Hadamard(), [1]),
        (CNOT(), [0, 1]),
        (Hadamard(), [0]),
        (Hadamard(), [1]),
    ],
)
outputSequence = Sequence([], [0, 1], [(CNOT(), [1, 0])])
lambdas = []

pat = Pattern("test3", inputSequence, outputSequence, lambdas)
print(pat)

Pattern #bits/#quits=0/2 and #lamdbas=0

seq = Sequence(
    [],
    [1, 0],
    [
        (Hadamard(), [0]),
        (Hadamard(), [1]),
        (CNOT(), [0, 1]),
        (Hadamard(), [0]),
        (Hadamard(), [1]),
    ],
)
newSeq, subst = pat.replacer(seq)
print("used subst=", subst)
print("newSeq=", newSeq)

check sequence
run ix= 0
set qubits 0 to value 0
res1/res2= True {}
run ix= 1
set qubits 1 to value 1
res1/res2= True {}
run ix= 2
res1/res2= True {}
run ix= 3
res1/res2= True {}
run ix= 4
res1/res2= True {}
res1/res2/resQ/resC= True {} {0: 0, 1: 1} {}
replace_recursion called for Sequence([], [0, 1], [(CNOT(), [1, 0])])
replace_recursion called for CNOT()
used subst= {}
newSeq= Sequence([], [0, 1], [(CNOT(), [1, 0])])

4.4.5. Example: Reverse BasicGate and InverseBasicGate

• the order of a BasicGate and an InverseBasicGate can be reversed if both have the same name

• both correspond to unitaries \(U\) and \(U^\dagger\), which commute

inputSequence = Sequence(
    [], [0], [(BasicGate("X1", 1), [0]), (InverseBasicGate("X1", 1), [0])]
)
outputSequence = Sequence(
    [], [0], [(InverseBasicGate("X1", 1), [0]), (BasicGate("X1", 1), [0])]
)
lambdas = []

pat = Pattern("test4", inputSequence, outputSequence, lambdas)
print(pat)

Pattern #bits/#quits=0/1 and #lamdbas=0

seq = Sequence(
    [], ["a"], [(BasicGate("u", 1), ["a"]), (InverseBasicGate("u", 1), ["a"])]
)
newSeq, subst = pat.replacer(seq)
print("used subst=", subst)
print("newSeq=", newSeq)

check sequence
run ix= 0
set qubits 0 to value a
check basic gate
add pattern.name/target.name= X1 u
res1/res2= True {'X1': 'u'}
run ix= 1
check basic gate
res1/res2= True {'X1': 'u'}
res1/res2/resQ/resC= True {'X1': 'u'} {0: 'a'} {}
replace_recursion called for Sequence([], [0], [(InverseBasicGate("X1", 1), [0]), (BasicGate("X1", 1), [0])])
replace_recursion called for InverseBasicGate("X1", 1)
replace inverse basic gate
replace_recursion called for BasicGate("X1", 1)
replace basic gate
used subst= {'X1': 'u'}
newSeq= Sequence([], ['a'], [(InverseBasicGate("u", 1), ['a']), (BasicGate("u", 1), ['a'])])

4.4.6. Finding candidates in a given sequence

• assume that we want to find sub-circuits on two qubits

• if a qubit has a gate with an outsider qubit then it is burned

# The first qubit should lead to two Hadamard gates.
# The second qubit should get burned because of the gate with qubit 2.
seq = Sequence(
    [],
    ["0", "1", "2"],
    [
        (Hadamard(), ["0"]),
        (Hadamard(), ["1"]),
        (CNOT(), ["1", "2"]),
        (Hadamard(), ["0"]),
    ],
)

findLongestRunSequence(seq, 0, ["0", "1"])

(Sequence([], ['0', '1'], [(Hadamard(), ['0']), (Hadamard(), ['1']), (Hadamard(), ['0'])]),
 [0, 1, 3])

4.4.7. A more complex example

seq = Sequence(
    [],
    [0, 1, 2, 3],
    [
        (Hadamard(), [0]),
        (CNOT(), [1, 2]),
        (CNOT(), [2, 3]),
        (CNOT(), [0, 2]),
        (Hadamard(), [0]),
        (Hadamard(), [1]),
    ],
)
findLongestRunSequence(seq, 0, [0, 1, 2])

(Sequence([], [0, 1, 2], [(Hadamard(), [0]), (CNOT(), [1, 2]), (Hadamard(), [1])]),
 [0, 1, 5])

4.4.8. Automatically applying the reversal pattern with gates in between

inputSequence = Sequence(
    [],
    [0, 1],
    [
        (Hadamard(), [0]),
        (Hadamard(), [1]),
        (CNOT(), [0, 1]),
        (Hadamard(), [0]),
        (Hadamard(), [1]),
    ],
)
outputSequence = Sequence([], [0, 1], [(CNOT(), [1, 0])])
lambdas = []

pat = Pattern("Hadamard upside-down", inputSequence, outputSequence, lambdas)
print(pat)

Pattern #bits/#quits=0/2 and #lamdbas=0

seq = Sequence(
    [],
    ["0", "1", "2", "3"],
    [
        (Hadamard(), ["0"]),
        (Hadamard(), ["2"]),
        (CNOT(), ["1", "3"]),
        (CNOT(), ["0", "2"]),
        (CNOT(), ["3", "1"]),
        (Hadamard(), ["0"]),
        (Hadamard(), ["2"]),
    ],
)
subseq, indexes = findLongestRunSequence(seq, 0, ["0", "2"])

print(subseq)
print(indexes)

Sequence([], ['0', '2'], [(Hadamard(), ['0']), (Hadamard(), ['2']), (CNOT(), ['0', '2']), (Hadamard(), ['0']), (Hadamard(), ['2'])])
[0, 1, 3, 5, 6]

newSeq, subst = pat.replacer(subseq)
print(newSeq)

check sequence
run ix= 0
set qubits 0 to value 0
res1/res2= True {}
run ix= 1
set qubits 1 to value 2
res1/res2= True {}
run ix= 2
res1/res2= True {}
run ix= 3
res1/res2= True {}
run ix= 4
res1/res2= True {}
res1/res2/resQ/resC= True {} {0: '0', 1: '2'} {}
replace_recursion called for Sequence([], [0, 1], [(CNOT(), [1, 0])])
replace_recursion called for CNOT()
Sequence([], ['0', '2'], [(CNOT(), ['2', '0'])])

4.4.9. Example: A CNOT reversal operation with other gates between

# The Hadamard conjugation of a CNOT leads to a flipped CNOT.

inputSequence = Sequence(
    [],
    [0, 1],
    [
        (Hadamard(), [0]),
        (Hadamard(), [1]),
        (CNOT(), [0, 1]),
        (Hadamard(), [0]),
        (Hadamard(), [1]),
    ],
)
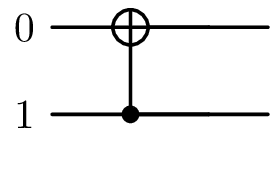
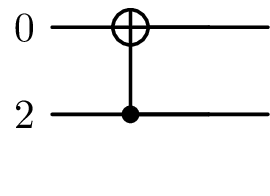
outputSequence = Sequence([], [0, 1], [(CNOT(), [1, 0])])
lambdas = []

pat = Pattern("Hadamard Upside-Down", inputSequence, outputSequence, lambdas)
print(pat)

Pattern #bits/#quits=0/2 and #lamdbas=0

sim = ensembleSimulatorSymPy(0, 3)
plot_latex(inputSequence, backend=sim, greek_symbol=True)

sim = ensembleSimulatorSymPy(0, 3)
plot_latex(outputSequence, backend=sim, greek_symbol=True)

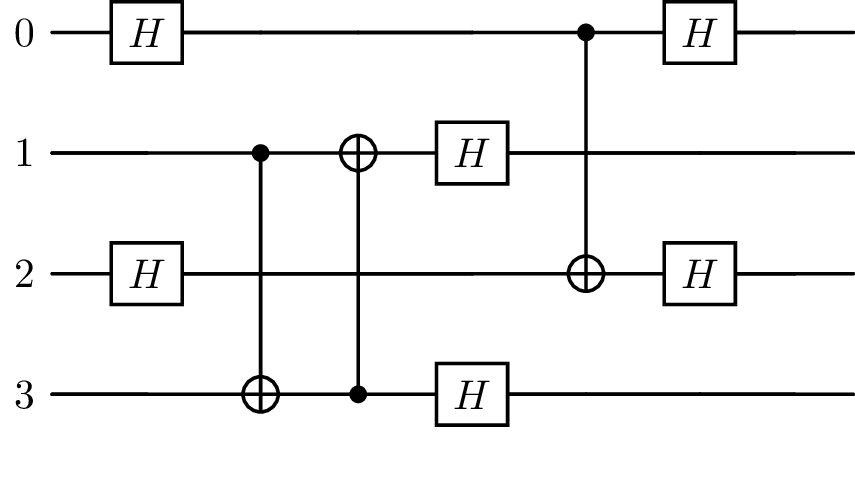
seq = Sequence(
    [],
    ["0", "1", "2", "3"],
    [
        (Hadamard(), ["0"]),
        (Hadamard(), ["2"]),
        (CNOT(), ["1", "3"]),
        (CNOT(), ["3", "1"]),
        (Hadamard(), ["1"]),
        (CNOT(), ["0", "2"]),
        (Hadamard(), ["0"]),
        (Hadamard(), ["3"]),
        (Hadamard(), ["2"]),
    ],
)

sim = ensembleSimulatorSymPy(0, 3)
plot_latex(seq, backend=sim, greek_symbol=True)

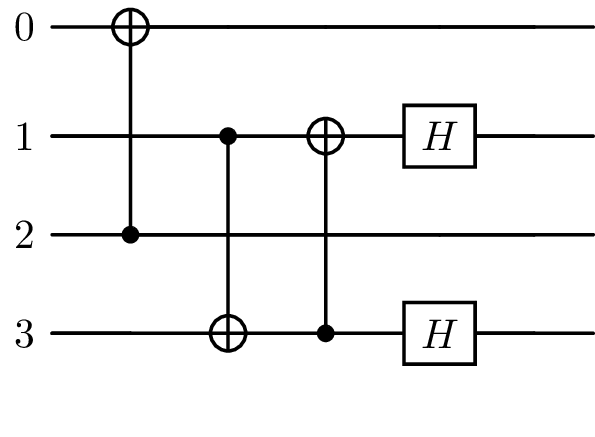
subseq, indexes = findLongestRunSequence(seq, 0, ["0", "2"])
print(subseq)
print(indexes)

Sequence([], ['0', '2'], [(Hadamard(), ['0']), (Hadamard(), ['2']), (CNOT(), ['0', '2']), (Hadamard(), ['0']), (Hadamard(), ['2'])])
[0, 1, 5, 6, 8]

newSeq, subst = pat.replacer(subseq)
print(newSeq)
print(subst)
sim = ensembleSimulatorSymPy(0, 3)
plot_latex(newSeq, backend=sim, greek_symbol=True)

check sequence
run ix= 0
set qubits 0 to value 0
res1/res2= True {}
run ix= 1
set qubits 1 to value 2
res1/res2= True {}
run ix= 2
res1/res2= True {}
run ix= 3
res1/res2= True {}
run ix= 4
res1/res2= True {}
res1/res2/resQ/resC= True {} {0: '0', 1: '2'} {}
replace_recursion called for Sequence([], [0, 1], [(CNOT(), [1, 0])])
replace_recursion called for CNOT()
Sequence([], ['0', '2'], [(CNOT(), ['2', '0'])])
{}

• Replace the gates in the original sequence directly

startIndex = 0  # We started here
print("we eliminate the indexes:", indexes)
newGatesAndTargets = []
for gi in range(len(seq.gatesAndTargets)):
    # The first hit with our pattern is replaces
    if gi == min(indexes):
        # We have to place the substitution circuit here.
        for g in newSeq.gatesAndTargets:
            print("place in:", g)
            newGatesAndTargets.append(g)

    if gi not in indexes:
        newGatesAndTargets.append(seq.gatesAndTargets[gi])

replacesSeq = Sequence(seq.bits, seq.qubits, newGatesAndTargets)

sim = ensembleSimulatorSymPy(0, 3)
plot_latex(replacesSeq, backend=sim, greek_symbol=True)

we eliminate the indexes: [0, 1, 5, 6, 8]
place in: (CNOT(), ['2', '0'])

4.4.10. Scan a whole circuit for a pattern

• the function getAllLongestRuns takes a sequence and a number of qubits as inputs

• the functions considers all possible combination of qubits with the specified number of qubits

• for each combination of qubits, the longest possible sequences on these qubits are returned

• a sequence cannot be extended on a qubit if there is a gate including a qubit, which is not part of the combination under consideration

• in the following example, we get the longest possible subsequences on all pairs of qubits

seq = Sequence(
    [],
    ["0", "1", "2", "3"],
    [
        (Hadamard(), ["0"]),
        (Hadamard(), ["2"]),
        (CNOT(), ["1", "3"]),
        (CNOT(), ["3", "1"]),
        (Hadamard(), ["1"]),
        (CNOT(), ["0", "2"]),
        (Hadamard(), ["0"]),
        (Hadamard(), ["3"]),
        (Hadamard(), ["2"]),
    ],
)
getAllLongestRuns(seq, 2)

[(('0', '1'), [0]),
 (('0', '1'), [4]),
 (('0', '1'), [6]),
 (('0', '2'), [0, 1, 5, 6, 8]),
 (('0', '3'), [0]),
 (('0', '3'), [7]),
 (('1', '2'), [1]),
 (('1', '2'), [4]),
 (('1', '2'), [8]),
 (('1', '3'), [2, 3, 4, 7]),
 (('2', '3'), [1]),
 (('2', '3'), [7]),
 (('2', '3'), [8])]

• in the following example, we get the longest possible sequences on single qubits

• the CNOT operation prevents sequences from being extended because the other qubit is used

seq = Sequence(
    [],
    ["0", "1"],
    [
        (Hadamard(), ["0"]),
        (Hadamard(), ["1"]),
        (CNOT(), ["0", "1"]),
        (Hadamard(), ["0"]),
        (Hadamard(), ["1"]),
        (Hadamard(), ["0"]),
    ],
)
sim = ensembleSimulatorSymPy(0, 3)
plot_latex(seq, backend=sim, greek_symbol=True)
getAllLongestRuns(seq, 1)

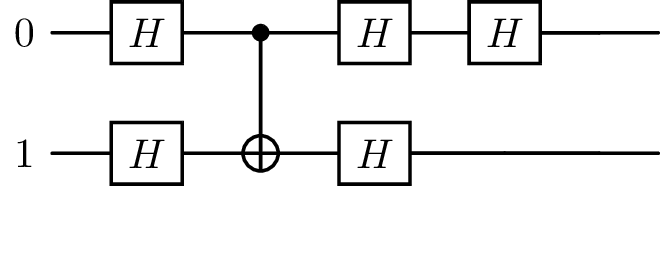
[(('0',), [0]), (('0',), [3, 5]), (('1',), [1]), (('1',), [4])]

• the result shows that only single Hadamard gates can be seen as a continuous sequence except for the two consecutive Hadamard gates on the first qubit

• in the following example, the function getAllRuns is used to get sequences on the specified number of qubits of a specific length

• this function is useful to find all possible candidates to apply a specific pattern, i.e. the number of qubits and gates can be specified

# The same as above, but we can ask for a length of the sub-sequence. For instance, if we have [0,1,2] as max.
# run and we have 2 as number of qubits, we get [0,1] and [1,2] at the end.
seq = Sequence(
    [],
    ["0", "1"],
    [
        (Hadamard(), ["0"]),
        (Hadamard(), ["1"]),
        (CNOT(), ["0", "1"]),
        (Hadamard(), ["0"]),
        (Hadamard(), ["1"]),
        (Hadamard(), ["0"]),
    ],
)
sim = ensembleSimulatorSymPy(0, 3)
plot_latex(seq, backend=sim, greek_symbol=True)
getAllRuns(seq, 2, 4, True)

scan qubits ('0', '1')
longest run: [0, 1, 2, 3, 4, 5]
processing candidate (('0', '1'), [0, 1, 2, 3, 4, 5]) len(candGates)/numberGates 6 4
new candidate: (('0', '1'), [0, 1, 2, 3])
new candidate: (('0', '1'), [1, 2, 3, 4])
new candidate: (('0', '1'), [2, 3, 4, 5])

[(('0', '1'), [0, 1, 2, 3]),
 (('0', '1'), [1, 2, 3, 4]),
 (('0', '1'), [2, 3, 4, 5])]

4.4.11. Example: Replacement of Toffoli gates

• a Toffoli gate can be decomposed into single qubit gates (Hadamard, \(T\) and \(T^\dagger\) gates) and 6 CNOT gates

• for instance, see https://en.wikipedia.org/wiki/Toffoli_gate#Related_logic_gates

• as an example, we replace three Toffoli gates step by step

• the Toffoli gates act on different qubits and the pattern matcher automatically adapts the patterns to the different qubits

from geqo.gates import Toffoli

inputSequence = Sequence([], [0, 1, 2], [(Toffoli(), [0, 1, 2])])
outputSequence = Sequence(
    [],
    [0, 1, 2],
    [
        (Hadamard(), [2]),
        (CNOT(), [1, 2]),
        (InverseBasicGate("pi4", 1), [2]),
        (CNOT(), [0, 2]),
        (BasicGate("pi4", 1), [2]),
        (CNOT(), [1, 2]),
        (InverseBasicGate("pi4", 1), [2]),
        (CNOT(), [0, 2]),
        (BasicGate("pi4", 1), [1]),
        (BasicGate("pi4", 1), [2]),
        (CNOT(), [0, 1]),
        (Hadamard(), [2]),
        (BasicGate("pi4", 1), [0]),
        (InverseBasicGate("pi4", 1), [1]),
        (CNOT(), [0, 1]),
    ],
)
lambdas = []

pat = Pattern(
    "toffoli",
    inputSequence,
    outputSequence,
    lambdas,
)
print(pat)

Pattern #bits/#quits=0/3 and #lamdbas=0

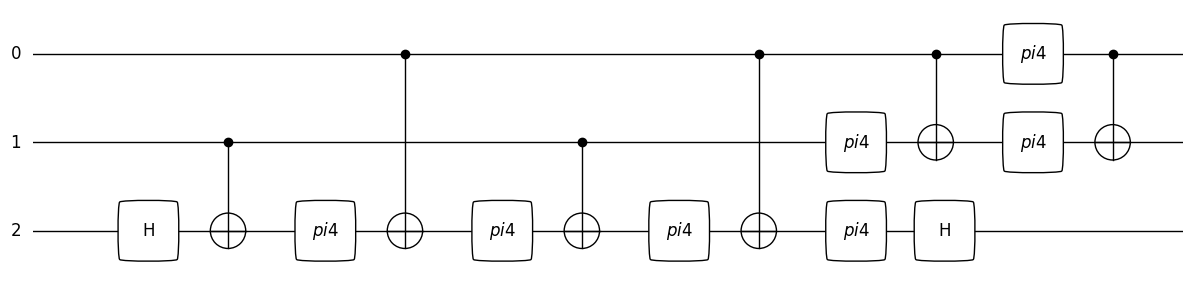
• in the following diagram, we visualize the gates that replace a Toffoli gate

• the BasicGates with the name pi/4 correspond to \(T\) gates

from geqo.visualization import plot_mpl

sim = ensembleSimulatorSymPy(0, 3)
plot_mpl(outputSequence, backend=sim, greek_symbol=True)

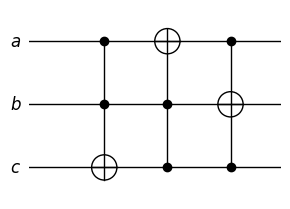
• we consider a sequence of 3 Toffoli gates

• each gate should be replaced by the replacement sequence

seq = Sequence(
    [],
    ["a", "b", "c"],
    [
        (Toffoli(), ["a", "b", "c"]),
        (Toffoli(), ["b", "c", "a"]),
        (Toffoli(), ["c", "a", "b"]),
    ],
)
sim = ensembleSimulatorSymPy(0, 3)
plot_mpl(seq, backend=sim, greek_symbol=True)

• we construct the replacement sequences for the first gate

• the qubits are matched automatically

• if there were parameters like rotation angles, these would also be matches automatically

newSeq1, subst1 = pat.replacer(
    Sequence([], ["a", "b", "c"], [(Toffoli(), ["a", "b", "c"])])
)

check sequence
run ix= 0
set qubits 0 to value a
set qubits 1 to value b
set qubits 2 to value c
res1/res2= True {}
res1/res2/resQ/resC= True {} {0: 'a', 1: 'b', 2: 'c'} {}
replace_recursion called for Sequence([], [0, 1, 2], [(Hadamard(), [2]), (CNOT(), [1, 2]), (InverseBasicGate("pi4", 1), [2]), (CNOT(), [0, 2]), (BasicGate("pi4", 1), [2]), (CNOT(), [1, 2]), (InverseBasicGate("pi4", 1), [2]), (CNOT(), [0, 2]), (BasicGate("pi4", 1), [1]), (BasicGate("pi4", 1), [2]), (CNOT(), [0, 1]), (Hadamard(), [2]), (BasicGate("pi4", 1), [0]), (InverseBasicGate("pi4", 1), [1]), (CNOT(), [0, 1])])
replace_recursion called for Hadamard()
replace_recursion called for CNOT()
replace_recursion called for InverseBasicGate("pi4", 1)
replace inverse basic gate
replace_recursion called for CNOT()
replace_recursion called for BasicGate("pi4", 1)
replace basic gate
replace_recursion called for CNOT()
replace_recursion called for InverseBasicGate("pi4", 1)
replace inverse basic gate
replace_recursion called for CNOT()
replace_recursion called for BasicGate("pi4", 1)
replace basic gate
replace_recursion called for BasicGate("pi4", 1)
replace basic gate
replace_recursion called for CNOT()
replace_recursion called for Hadamard()
replace_recursion called for BasicGate("pi4", 1)
replace basic gate
replace_recursion called for InverseBasicGate("pi4", 1)
replace inverse basic gate
replace_recursion called for CNOT()

• the replacement sequence for the first Toffoli gate is now stored in newSeq1

• with the following loop, the first gate of a matched pattern is replaced by the replacement sequence

• the further gates of a matched pattern are ignored, because the gates are replaced by other gates

indexes = [0]  # Replace the first Toffoli

startIndex = 0  # We started here
print("we eliminate the indexes:", indexes)
newGatesAndTargets = []
for gi in range(len(seq.gatesAndTargets)):
    # The first hit with our pattern is replaces
    if gi == min(indexes):
        # We have to place the substitution circuit here.
        for g in newSeq1.gatesAndTargets:
            print("place in:", g)
            newGatesAndTargets.append(g)

    if gi not in indexes:
        newGatesAndTargets.append(seq.gatesAndTargets[gi])

replacesSeq = Sequence(seq.bits, seq.qubits, newGatesAndTargets)

sim = ensembleSimulatorSymPy(0, 3)
plot_mpl(replacesSeq, backend=sim, greek_symbol=True)

we eliminate the indexes: [0]
place in: (Hadamard(), ['c'])
place in: (CNOT(), ['b', 'c'])
place in: (InverseBasicGate("pi4", 1), ['c'])
place in: (CNOT(), ['a', 'c'])
place in: (BasicGate("pi4", 1), ['c'])
place in: (CNOT(), ['b', 'c'])
place in: (InverseBasicGate("pi4", 1), ['c'])
place in: (CNOT(), ['a', 'c'])
place in: (BasicGate("pi4", 1), ['b'])
place in: (BasicGate("pi4", 1), ['c'])
place in: (CNOT(), ['a', 'b'])
place in: (Hadamard(), ['c'])
place in: (BasicGate("pi4", 1), ['a'])
place in: (InverseBasicGate("pi4", 1), ['b'])
place in: (CNOT(), ['a', 'b'])

• we now create the replacement gates for the second Toffoli gate

newSeq2, subst2 = pat.replacer(
    Sequence([], ["a", "b", "c"], [(Toffoli(), ["b", "c", "a"])])
)

check sequence
run ix= 0
set qubits 0 to value b
set qubits 1 to value c
set qubits 2 to value a
res1/res2= True {}
res1/res2/resQ/resC= True {} {0: 'b', 1: 'c', 2: 'a'} {}
replace_recursion called for Sequence([], [0, 1, 2], [(Hadamard(), [2]), (CNOT(), [1, 2]), (InverseBasicGate("pi4", 1), [2]), (CNOT(), [0, 2]), (BasicGate("pi4", 1), [2]), (CNOT(), [1, 2]), (InverseBasicGate("pi4", 1), [2]), (CNOT(), [0, 2]), (BasicGate("pi4", 1), [1]), (BasicGate("pi4", 1), [2]), (CNOT(), [0, 1]), (Hadamard(), [2]), (BasicGate("pi4", 1), [0]), (InverseBasicGate("pi4", 1), [1]), (CNOT(), [0, 1])])
replace_recursion called for Hadamard()
replace_recursion called for CNOT()
replace_recursion called for InverseBasicGate("pi4", 1)
replace inverse basic gate
replace_recursion called for CNOT()
replace_recursion called for BasicGate("pi4", 1)
replace basic gate
replace_recursion called for CNOT()
replace_recursion called for InverseBasicGate("pi4", 1)
replace inverse basic gate
replace_recursion called for CNOT()
replace_recursion called for BasicGate("pi4", 1)
replace basic gate
replace_recursion called for BasicGate("pi4", 1)
replace basic gate
replace_recursion called for CNOT()
replace_recursion called for Hadamard()
replace_recursion called for BasicGate("pi4", 1)
replace basic gate
replace_recursion called for InverseBasicGate("pi4", 1)
replace inverse basic gate
replace_recursion called for CNOT()

• we replace the first remaining Toffoli gate with the appropriate sequence

indexes = [15]  # Replace the first Toffoli

startIndex = 0  # We started here
print("we eliminate the indexes:", indexes)
newGatesAndTargets = []
for gi in range(len(replacesSeq.gatesAndTargets)):
    # The first hit with our pattern is replaces
    if gi == min(indexes):
        # We have to place the substitution circuit here.
        for g in newSeq2.gatesAndTargets:
            print("place in:", g)
            newGatesAndTargets.append(g)

    if gi not in indexes:
        newGatesAndTargets.append(replacesSeq.gatesAndTargets[gi])

replacesSeq = Sequence(replacesSeq.bits, replacesSeq.qubits, newGatesAndTargets)

sim = ensembleSimulatorSymPy(0, 3)
plot_mpl(replacesSeq, backend=sim, greek_symbol=True)

we eliminate the indexes: [15]
place in: (Hadamard(), ['a'])
place in: (CNOT(), ['c', 'a'])
place in: (InverseBasicGate("pi4", 1), ['a'])
place in: (CNOT(), ['b', 'a'])
place in: (BasicGate("pi4", 1), ['a'])
place in: (CNOT(), ['c', 'a'])
place in: (InverseBasicGate("pi4", 1), ['a'])
place in: (CNOT(), ['b', 'a'])
place in: (BasicGate("pi4", 1), ['c'])
place in: (BasicGate("pi4", 1), ['a'])
place in: (CNOT(), ['b', 'c'])
place in: (Hadamard(), ['a'])
place in: (BasicGate("pi4", 1), ['b'])
place in: (InverseBasicGate("pi4", 1), ['c'])
place in: (CNOT(), ['b', 'c'])

• we create the replacement sequence for the remaining Toffoli gate

newSeq3, subst3 = pat.replacer(
    Sequence([], ["a", "b", "c"], [(Toffoli(), ["c", "a", "b"])])
)

check sequence
run ix= 0
set qubits 0 to value c
set qubits 1 to value a
set qubits 2 to value b
res1/res2= True {}
res1/res2/resQ/resC= True {} {0: 'c', 1: 'a', 2: 'b'} {}
replace_recursion called for Sequence([], [0, 1, 2], [(Hadamard(), [2]), (CNOT(), [1, 2]), (InverseBasicGate("pi4", 1), [2]), (CNOT(), [0, 2]), (BasicGate("pi4", 1), [2]), (CNOT(), [1, 2]), (InverseBasicGate("pi4", 1), [2]), (CNOT(), [0, 2]), (BasicGate("pi4", 1), [1]), (BasicGate("pi4", 1), [2]), (CNOT(), [0, 1]), (Hadamard(), [2]), (BasicGate("pi4", 1), [0]), (InverseBasicGate("pi4", 1), [1]), (CNOT(), [0, 1])])
replace_recursion called for Hadamard()
replace_recursion called for CNOT()
replace_recursion called for InverseBasicGate("pi4", 1)
replace inverse basic gate
replace_recursion called for CNOT()
replace_recursion called for BasicGate("pi4", 1)
replace basic gate
replace_recursion called for CNOT()
replace_recursion called for InverseBasicGate("pi4", 1)
replace inverse basic gate
replace_recursion called for CNOT()
replace_recursion called for BasicGate("pi4", 1)
replace basic gate
replace_recursion called for BasicGate("pi4", 1)
replace basic gate
replace_recursion called for CNOT()
replace_recursion called for Hadamard()
replace_recursion called for BasicGate("pi4", 1)
replace basic gate
replace_recursion called for InverseBasicGate("pi4", 1)
replace inverse basic gate
replace_recursion called for CNOT()

• finally, we can replace the last of the Toffoli gates with the sequence

indexes = [30]  # Replace the first Toffoli

startIndex = 0  # We started here
print("we eliminate the indexes:", indexes)
newGatesAndTargets = []
for gi in range(len(replacesSeq.gatesAndTargets)):
    # The first hit with our pattern is replaces
    if gi == min(indexes):
        # We have to place the substitution circuit here.
        for g in newSeq3.gatesAndTargets:
            print("place in:", g)
            newGatesAndTargets.append(g)

    if gi not in indexes:
        newGatesAndTargets.append(replacesSeq.gatesAndTargets[gi])

replacesSeq = Sequence(replacesSeq.bits, replacesSeq.qubits, newGatesAndTargets)

sim = ensembleSimulatorSymPy(0, 3)
plot_mpl(replacesSeq, backend=sim, greek_symbol=True)

we eliminate the indexes: [30]
place in: (Hadamard(), ['b'])
place in: (CNOT(), ['a', 'b'])
place in: (InverseBasicGate("pi4", 1), ['b'])
place in: (CNOT(), ['c', 'b'])
place in: (BasicGate("pi4", 1), ['b'])
place in: (CNOT(), ['a', 'b'])
place in: (InverseBasicGate("pi4", 1), ['b'])
place in: (CNOT(), ['c', 'b'])
place in: (BasicGate("pi4", 1), ['a'])
place in: (BasicGate("pi4", 1), ['b'])
place in: (CNOT(), ['c', 'a'])
place in: (Hadamard(), ['b'])
place in: (BasicGate("pi4", 1), ['c'])
place in: (InverseBasicGate("pi4", 1), ['a'])
place in: (CNOT(), ['c', 'a'])

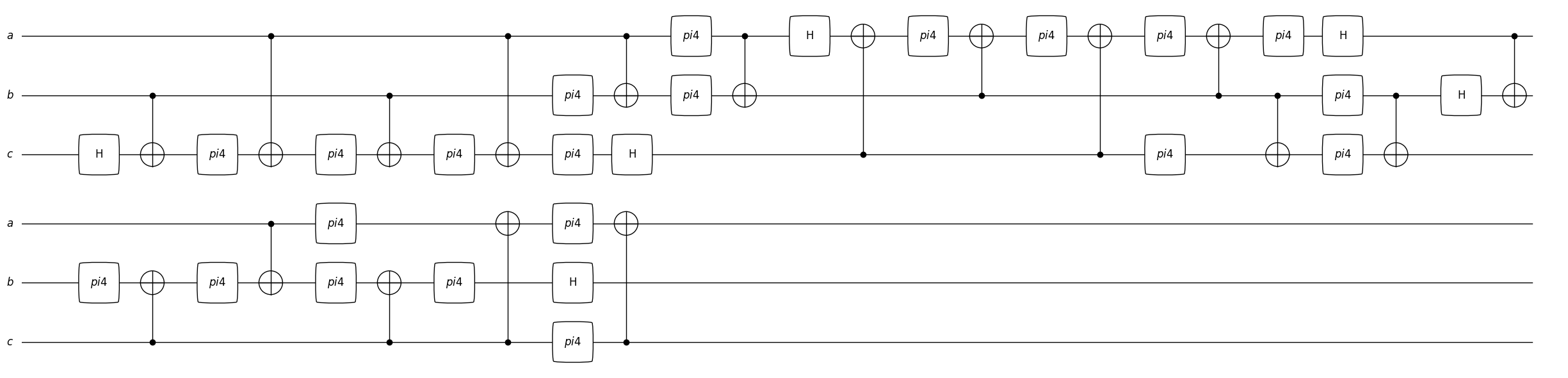
• the result shows that the qubits of the replacement pattern of a Toffoli gate were automatically matched with the corresponding qubits of the Toffoli gates